OEF Optimisation linéaire --- Introduction ---

Ce module regroupe pour l'instant 44 exercices sur l'optimisation linéaire : méthode graphique (G), méthode du simplexe (S ou Simplexe), dualité (MD). Des exemples concrets à modéliser ont été utilisés. Les exercices G* et MD* demandent uniquement les résultats finaux.

Ces exercices ont été faits pour des étudiants d'IUT (logistique du transport).

MD: Exploitation agricole

Quelles sont les quantités optimales de et de à utiliser par hectare si le prix des paquets est de euros pour A et de euros pour ?
Engrais A
Engrais B
Les quantités optimales de et sont en effet de et de paquets si le prix des paquets est de euros pour A et de euros pour .
Une entreprise de chimie propose à l'exploitant agricole de lui vendre directement et en vrac l'ensemble du calcium, du sodium, et du potassium dont il a besoin. On note respectivement , , le prix, à fixer, d'un kilo de potassium, d'un kilo de calcium, d'un kilo de sodium.
Déterminer en fonction de , ,
L'affaire sera conclue si le prix de l'équivalent d'un paquet A et celui d'un paquet B ne dépassent pas les prix initiaux d'un paquet A et d'un paquet B.

Contrainte pour A :

Contrainte pour B :

L'entreprise de chimie cherche à maximiser son chiffre d'affaires par hectare :

Max =

Finalement ??

Simplexe : variables artificielles

On applique la méthode des variables artificielles pour le résoudre.

On utilise la lettre pour désigner un nombre très grand.

Quelles variables d'écart faut-il introduire ?

Quelles variables artificielles faut-il introduire

Quelles sont les variables rentrées ?

Donner les variables dans l'ordre croissant de leur numéro.

Remplir le premier tableau du simplexe:
Résultats
 

S: Variables artificielles
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

Simplexe : Variables rentrées ou sorties

Donner la liste des variables rentrées :

Donner la liste des variables sorties :

Quelle est la variable rentrante :

Quelle est la variable sortante :

Simplexe : Variables rentrées

Compléter la colonne de gauche.

Simplexe : Conclure à partir du dernier tableau

Voici le dernier tableau d'un problème d'optimisation linéaire.
Que pouvez-vous conclure ?
La fonction économique est optimale pour les valeurs suivantes et vaut

Simplexe : un tableau

On le résoud par la méthode du simplexe.

Le premier tableau de Un tableau obtenu en faisant tourner l'algorithme du simplexe est

Quelle est la variable rentrante :

Consigne : Ecrire x7 pour la variable par exemple.
La variable rentrante est . Complétez maintenant la colonne des contraintes :
Résultats
  Z +
Consigne : Ecrire x s'il n'y a pas de contrainte et inf si la contrainte est infinie
Quelle est la variable sortante :

La variable rentrante est , la variable sortante est . On échange donc avec dans la première colonne. Remplissez maintenant la ligne du pivot
Résultats
to    
   
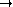
Consigne : Ecrire x7 pour la variable par exemple. Remplissez les autres lignes
Résultats
  Z +

Simplexe : Un tableau (var. art.)

On le résoud par la méthode du simplexe.

Le premier tableau de Un tableau obtenu en faisant tourner l'algorithme du simplexe est

Quelle est la variable rentrante :

Consigne : Ecrire x7 pour la variable par exemple.
La variable rentrante est . Complétez maintenant la colonne des contraintes :
Résultats
  Z +
Consigne : Ecrire x s'il n'y a pas de contrainte et inf si la contrainte est infinie
Quelle est la variable sortante :

La variable rentrante est , la variable sortante est . On échange donc avec dans la première colonne. Remplissez maintenant la ligne du pivot
Résultats
to    
   
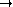
Consigne : Ecrire x7 pour la variable par exemple. Remplissez les autres lignes
Résultats
  Z +

MD : Dualité

Le problème dual a variables et contraintes.
On note 1 , s les variables du problème dual. Ecrire la fonction objectif

omega =

La fonction à optimiser dans le programme dual est omega = .
Compléter pour obtenir les contraintes :

G : Chaussette de laine et de coton

Pour y répondre, commencer par répondre aux questions dans la colonne de droite.
Les droites de contrainte ont été placées sur le dessin. Cliquer à l'intérieur du polygone des contraintes.

Donner les coordonnées des sommets du polygone des contraintes :
  • Point s :

La droite rouge est la droite de bénéfice 0. Donner son équation :

Donner le numéro du point extrémal en lequel est obtenue l'optimisation :

En conclusion, avec et , .

S: Chaussettes de laine et de coton
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

G : Des problèmes de trains

Pour y répondre, commencer par répondre aux questions dans la colonne de droite.
Les droites de contrainte ont été placées sur le dessin. Cliquer à l'intérieur du polygone des contraintes.

Donner les coordonnées des sommets du polygone des contraintes :
  • Point s :

La droite rouge est la droite de bénéfice 0. Donner son équation :

Donner le numéro du point extrémal en lequel est obtenue l'optimisation :

En conclusion, avec et , .

S: Des problèmes de trains
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

G : Produits dangereux

Pour y répondre, commencer par répondre aux questions dans la colonne de droite.
Les droites de contrainte ont été placées sur le dessin. Cliquer à l'intérieur du polygone des contraintes.

Donner les coordonnées des sommets du polygone des contraintes :
  • Point s :

La droite rouge est la droite de bénéfice 0. Donner son équation :

Donner le numéro du point extrémal en lequel est obtenue l'optimisation :

En conclusion, avec et , .

G : Productions

Pour y répondre, commencer par répondre aux questions dans la colonne de droite.
Les droites de contrainte ont été placées sur le dessin. Cliquer à l'intérieur du polygone des contraintes.

Donner les coordonnées des sommets du polygone des contraintes :
  • Point s :

La droite rouge est la droite de bénéfice 0. Donner son équation :

Donner le numéro du point extrémal en lequel est obtenue l'optimisation :

En conclusion, avec et , .

S: Productions
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

G : Production optimale

Pour y répondre, commencer par répondre aux questions dans la colonne de droite.
Les droites de contrainte ont été placées sur le dessin. Cliquer à l'intérieur du polygone des contraintes.

Donner les coordonnées des sommets du polygone des contraintes :
  • Point s :

La droite rouge est la droite de bénéfice 0. Donner son équation :

Donner le numéro du point extrémal en lequel est obtenue l'optimisation :

En conclusion, avec et , .

S: Production optimale
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

G : Bretelles

Pour y répondre, commencer par répondre aux questions dans la colonne de droite.
Les droites de contrainte ont été placées sur le dessin. Cliquer à l'intérieur du polygone des contraintes.

Donner les coordonnées des sommets du polygone des contraintes :
  • Point s :

La droite rouge est la droite de bénéfice 0. Donner son équation :

Donner le numéro du point extrémal en lequel est obtenue l'optimisation :

En conclusion, avec et , .

G : Bretelles

= -- -- ---

Pour y répondre, commencer par répondre aux questions dans la colonne de droite.
Les droites de contrainte ont été placées sur le dessin. Cliquer à l'intérieur du polygone des contraintes.

Donner les coordonnées des sommets du polygone des contraintes :
  • Point s :

La droite rouge est la droite de bénéfice 0. Donner son équation :

Donner le numéro du point extrémal en lequel est obtenue l'optimisation :

En conclusion, avec et , .

S: Bretelles
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

G : Articles

Pour y répondre, commencer par répondre aux questions dans la colonne de droite.
Les droites de contrainte ont été placées sur le dessin. Cliquer à l'intérieur du polygone des contraintes.

Donner les coordonnées des sommets du polygone des contraintes :
  • Point s :

La droite rouge est la droite de bénéfice 0. Donner son équation :

Donner le numéro du point extrémal en lequel est obtenue l'optimisation :

En conclusion, avec et , .

S: Articles
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

S: Production de trois articles
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

MD: Conditionnement

Remplir le premier tableau du simplexe dual :
Résultats
Objectifs Z +
On fait tourner l'algorithme du simplexe dual.
Dans le tableau de l'algorithme du simplexe dual, calculer la ligne des objectifs :
Z +
La ligne des gains du tableau suivant est
Résultats
 
  Z
La solution optimale du problème primal est

MD: Campagne publicitaire

Remplir le premier tableau du simplexe dual :
Résultats
Objectifs Z +
On fait tourner l'algorithme du simplexe dual.
Dans le tableau de l'algorithme du simplexe dual, calculer la ligne des objectifs :
Z +
La ligne des gains du tableau suivant est
Résultats
 
  Z
La solution optimale du problème primal est

MD: Cosmétique

Remplir le premier tableau du simplexe dual :
Résultats
Objectifs Z +
On fait tourner l'algorithme du simplexe dual.
Dans le tableau de l'algorithme du simplexe dual, calculer la ligne des objectifs :
Z +
La ligne des gains du tableau suivant est
Résultats
 
  Z
La solution optimale du problème primal est

S: Programmation linéaire (tableau)
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

S: Méthode du simplexe
En appliquant la méthode du simplexe, on obtient le premier tableau suivant :
La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante. La variable artificielle est sortie, on n'a plus besoin de calculer la colonne correspondante.
Remplissez les lignes demandées du tableau suivant obtenu en utilisant l'algorithme du simplexe :
Résultats
             
 
Donner les valeurs des variables à la fin de l'algorithme

G : Programmation linéaire

Pour y répondre, commencer par répondre aux questions dans la colonne de droite.
Les droites de contrainte ont été placées sur le dessin. Cliquer à l'intérieur du polygone des contraintes.

Donner les coordonnées des sommets du polygone des contraintes :
  • Point s :

La droite rouge est la droite de bénéfice 0. Donner son équation :

Donner le numéro du point extrémal en lequel est obtenue l'optimisation :

En conclusion, avec et , .

Simplexe : Trouver le pivot

Cliquer sur le pivot :

Simplexe : Est-ce la fin

L'algorithme est-il terminé ?

Quelle solution réalisable obtient-on ? La fonction économique vaut alors

MD: Méthode du dual

Remplir le premier tableau du simplexe dual :
Résultats
Objectifs Z +
On fait tourner l'algorithme du simplexe dual.
Dans le tableau de l'algorithme du simplexe dual, calculer la ligne des objectifs :
Z +
La ligne des gains du tableau suivant est
Résultats
 
  Z
La solution optimale du problème primal est
The most recent version
Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.